20+ P-Adic Numbers Pdf
5 5 1The set of all rational numbers also referred to as the rationals the field of rationals or the field of rational numbers is. Any base is possible but a prime number base provides the best mathematical properties.

Fractions And P Adic Numbers Real Numbers And Limits Math Foundations 90 N J Wildberger Youtube
This turns the set L R M N.

. PDF Comments NEW. This was first proved by Gauss. Web Discrete mathematics is the study of mathematical structures that can be considered discrete in a way analogous to discrete variables having a bijection with the set of natural numbers rather than continuous analogously to continuous functionsObjects studied in discrete mathematics include integers graphs and statements in logic.
Web Rational numbers have been widely used a long time before the elaboration of the concept of field. By testing the values of these numbers modulo one. The number system that results depends on what base is used for the digits.
This algorithm works equally well in the p-adic numbers but cannot be used to identify real square roots with p-adic square roots. The negative numbers are the additive inverses of the corresponding positive numbers. Exactly when n is a prime number.
This can be proved by using the asymptotic growth of the central binomial coefficients by Stirlings approximation for or via generating functions. Web The search of the solution may be made dramatically faster by sieving. Web Browse our listings to find jobs in Germany for expats including jobs for English speakers or those in your native language.
Web Complex analysis traditionally known as the theory of functions of a complex variable is the branch of mathematical analysis that investigates functions of complex numbersIt is helpful in many branches of mathematics including algebraic geometry number theory analytic combinatorics applied mathematics. Web In mathematics a Fermat number named after Pierre de Fermat who first studied them is a positive integer of the form where n is a non-negative integer. N 3 n n 2 n n n.
Web in the sense that the quotient of the nth Catalan number and the expression on the right tends towards 1 as n approaches infinity. Transposing the square root is x -190y2010. They are named after James Stirling who introduced them in a purely algebraic setting in his book Methodus differentialis 1730.
Web A pentagonal number is a figurate number that extends the concept of triangular and square numbers to the pentagon but unlike the first two the patterns involved in the construction of pentagonal numbers are not rotationally symmetricalThe nth pentagonal number p n is the number of distinct dots in a pattern of dots consisting of the outlines of. 3 5 17 257 65537 4294967297 18446744073709551617 sequence A000215 in the OEIS. Web Résidence officielle des rois de France le château de Versailles et ses jardins comptent parmi les plus illustres monuments du patrimoine mondial et constituent la plus complète réalisation de lart français du XVIIe siècle.
This means that for these n. The set of natural numbers is a. Web A near-optimal hyperbolic approximation to x 2 on the interval is y19010-x-20.
Web A prime number or a prime is a natural number greater than 1 that is not a product of two smaller natural numbers. G is a functor from the category of abelian groups to itself. For example 3 7 is a rational number as is every integer eg.
Web Gauss 1799 showed however that complex differential equations require complex numbers. They were rediscovered and given a combinatorial meaning by Masanobu Saka in 1782. PDF Comments NEW.
Web The Betti numbers of X are the sum of the Hodge numbers in a given row. The reals and the p-adic numbers are the completions of the rationals. Web In arithmetic and algebra the cube of a number n is its third power that is the result of multiplying three instances of n together.
Web In 1897 Kurt Hensel introduced p-adic numbers. Every year thousands of new PhDs in mathematics were awarded and jobs were available in both teaching and industry. Web Generalizations and related concepts.
2022-03-20 Anabelian Geometry the Geometry of Categories 1 The Profinite Grothendieck Conjecture for Closed Hyperbolic Curves over Number Fields. A basic application of Hodge theory is then that the odd Betti numbers b 2a1 of a smooth complex projective variety or compact Kähler manifold are even by Hodge symmetry. Web In mathematics Stirling numbers arise in a variety of analytic and combinatorial problems.
The cube of a number or any other mathematical expression is denoted by a superscript 3 for example 2 3 8 or x 1 3. Suppose D is a Dedekind domain and E is its field of fractionsPick a non-zero prime ideal P of DIf x is a. Web 2022-03-20 3 An Introduction to p-adic Teichmuller Theory.
In the language of mathematics the set of integers is often denoted by the boldface Z or blackboard bold. A natural number greater than 1 that is not prime is called a composite numberFor example 5 is prime because the only ways of writing it as a product 1 5 or 5 1 involve 5 itselfHowever 4 is composite because it is a product 2 2 in. Hence analysts began to substitute the study of functions thus opening a new and fertile field.
Web The p-adic numbers may have infinitely long expansions to the left of the decimal point in the same way that real numbers may have infinitely long expansions to the right. Cauchy was the first to appreciate the importance of this view. The cube is also the number multiplied by its square.
For M and N fixed the map G L R M N. If 2 k 1 is prime and k 0 then k must be a power of 2 so 2 k. This is not true for compact complex manifolds in general as shown by the example of the Hopf.
Two different sets of numbers bear this name. For example 11 represents the number. The abstractly required.
Thereafter the real question was no longer whether a solution is possible by means of known. It is also possible to complete other fields for instance general algebraic number fields in an analogous wayThis will be described now. An effort to catalogue the areas and applications of mathematics was undertaken in Kleins.
2012-12-20 2 A Version of the Grothendieck Conjecture for p-adic. As well as in physics including the. That is a mathematical notation for representing numbers of a given set using digits or other symbols in a consistent manner.
Where By definition the group is cyclic if and only if it has a generator g a generating set g of size one that is the powers give all possible. Web An integer is the number zero a positive natural number 1 2 3 etc or a negative integer with a minus sign 1 2 3 etc. The only Catalan numbers C n that are odd are those for which n 2 k 1.
The same sequence of symbols may represent different numbers in different numeral systems. Web The set of all such balanced products over R from M N to G is denoted by L R M N. The first few Fermat numbers are.
The cube function is the. Web A numeral system or system of numeration is a writing system for expressing numbers. They are numbers that can be written as fractions ab where a and b are integers and b 0The additive inverse of such a fraction is ab and the multiplicative inverse provided that a 0 is ba which can be seen as follows.
Web In mathematics a rational number is a number that can be expressed as the quotient or fraction p q of two integers a numerator p and a non-zero denominator q. For this method we suppose without loss of generality that if it were not the case it would suffice to replace each by the remainder of its division by This implies that the solution belongs to the arithmetic progression. Web The group is cyclic if and only if n is 1 2 4 p k or 2p k where p is an odd prime and k 0For all other values of n the group is not cyclic.
G into an abelian group. In other words any number n is a prime number if. Web In algebra and number theory Wilsons theorem states that a natural number n 1 is a prime number if and only if the product of all the positive integers less than n is one less than a multiple of nThat is using the notations of modular arithmetic the factorial.
The 20th century saw mathematics become a major profession. If φ ψ are balanced products then each of the operations φ ψ and φ defined pointwise is a balanced product.

Pdf Constructing Totally P Adic Numbers Of Small Height

Pdf Rational Base Number Systems For P Adic Numbers Semantic Scholar

P Adic Number Wikipedia

P Adic Analysis Essential Ideas And Results Chapter 1 Ultrametric Pseudodifferential Equations And Applications

P Adic Numbers Part 2 P Adic Powers Youtube

P Adic Valued Distributions In Mathematical Physics Springerlink
What Even Is Distance P Adic Numbers And Completion Of The Set Of Real Numbers 3010tangents

P Adic Numbers Springerlink

P Adic Numbers P Adic Analysis And Zeta Functions Springerlink

P Adic Mathematics And Theoretical Biology Sciencedirect

Pdf A Formal Proof Of Hensel S Lemma Over The P Adic Integers Semantic Scholar
The Numbers Behind A Fields Medalist S Math Scientific American Blog Network

Pdf Euclidean Models Of The P Adic Integers Semantic Scholar

P Adic Numbers Chapter 1 Theory Of P Adic Distributions
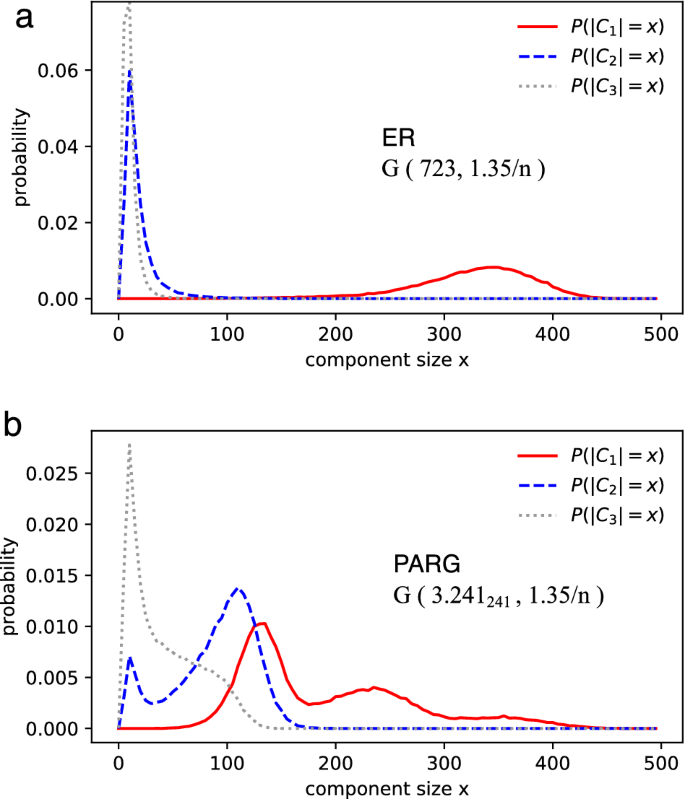
P Adic Numbers Encode Complex Networks Scientific Reports

Pdf The P Adic Numbers Akhil Mathew Academia Edu

An Infinite Universe Of Number Systems Quanta Magazine